Simulating Stokes' Law Visually

I built a simple application to teach factors affecting the floating and sedimentation of particles in liquid.

Update

Since this blog was posted I published an article on the Stokes' Law simulation in the Journal of Chemical Education. Read it for free here.

Many food processes are designed to either promote or prevent the physical separation of particles from liquids. The behaviour governing such separation phenomena is described using an equation known as Stokes' Law. Students of food science are familiar with this equation, although it is commonly misunderstood. Technical fixes for the physical instabilities in liquid foods are simple and long-standing, yet are sometimes mistrusted by the public. This short post discusses this equation and a simple interactive animation for developing intuition around the phenomena it describes.

Animating Stokes' Law#

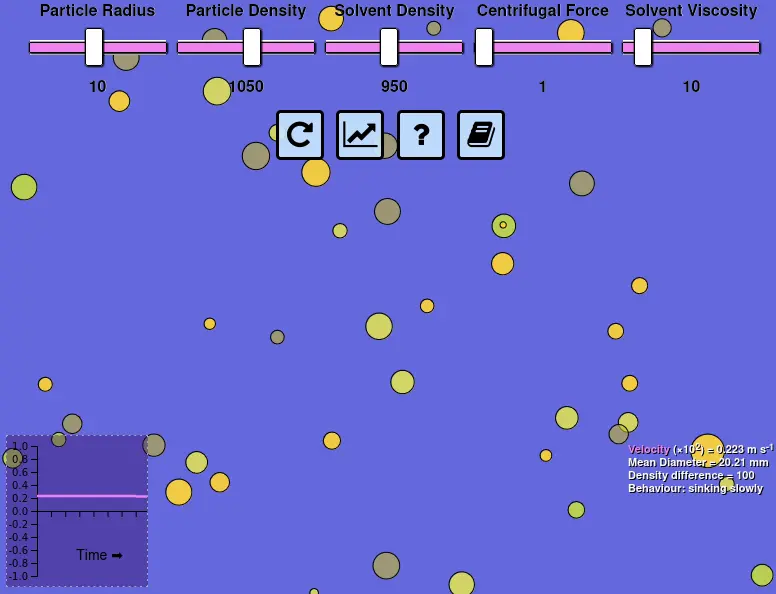User interface for Stokes' Law simulation showing sliders (top), velocity graph (bottom-left) and statistics (bottom-right). View interactive simulation in full screen or read the source code to see the JavaScript implementation (if you're so inclined)

Stokes' Law describes the sedimentation of particles in suspensions (fruit pulp in orange juice) and the flotation of droplets in emulsions (creaming of milk fat). In food science it is invoked for a variety of purposes. One of the most simple techniques for measuring a liquid's viscosity involves using Stokes' Law to estimate the value from the rate at which a ball falls through the liquid. The equation is also used to identify the key parameters that influence how a group of particles fall or rise due to gravity, which can be used to develop strategies to make it happen quicker or slower. A version of the equation is shown below describing the separation velocity ($v$) of particles with diameter $D$ in a solvent with viscosity $\mu$ when subject to acceleration due to gravity $g$. The $\Delta \rho$ means the difference ($\Delta$) between the density ($\rho$) of the particle and the solvent.

$$v = \frac{D^2 \cdot(\Delta \rho) \cdot g }{18 \cdot \mu}$$

Techno-functionality#

Some of the technological solutions informed by Stokes' Law are the source of routine confusion when "homogenised" is found on a product label or "guar gum" is seen in an ingredients list. Homogenisation is simply a way of physically reducing the size of particles. As the particle diameter value ($D$) in Stokes' Law is raised to the power of $2$ it has a significant influence on separation speed. Guar gum is one of a variety of food ingredients that has a purely techno-functional role, which typically involves increasing viscosity ($\mu$) so that friction slows particles down as they move through the liquid. Sometimes it might be desirable to promote instability, such as when whole milk is centrifuged to separate cream from skim milk, replacing the acceleration due to gravity ($g$) with that caused by centrifugal force ($\omega ^2 r$). These factors become more obvious if you play around with the particle diameter and solvent viscosity sliders in the animation. Try the other sliders and you might find some other interesting effects.

Intuition and Science#

Most of us have a good intuition for these phenomena in an everyday context. We expect large stones to sink faster than small pebbles. We know that the air pockets in a wine bottle cork means that it will tend to float on water. In food, the particles involved are often microscopic, making the behavior less salient. Showing a static photograph of particles on a microscope slide does not give us a feel for the dynamics involved. If we are uncomfortable with equations then the mathematics of Stokes' Law might not help. That's why I developed a simple simulation that allows students to manipulate all of the major variables using sliders. I hope this simple "virtual experiment" can improve the intuition of students for the phenomena but also the equation that helps explain them.

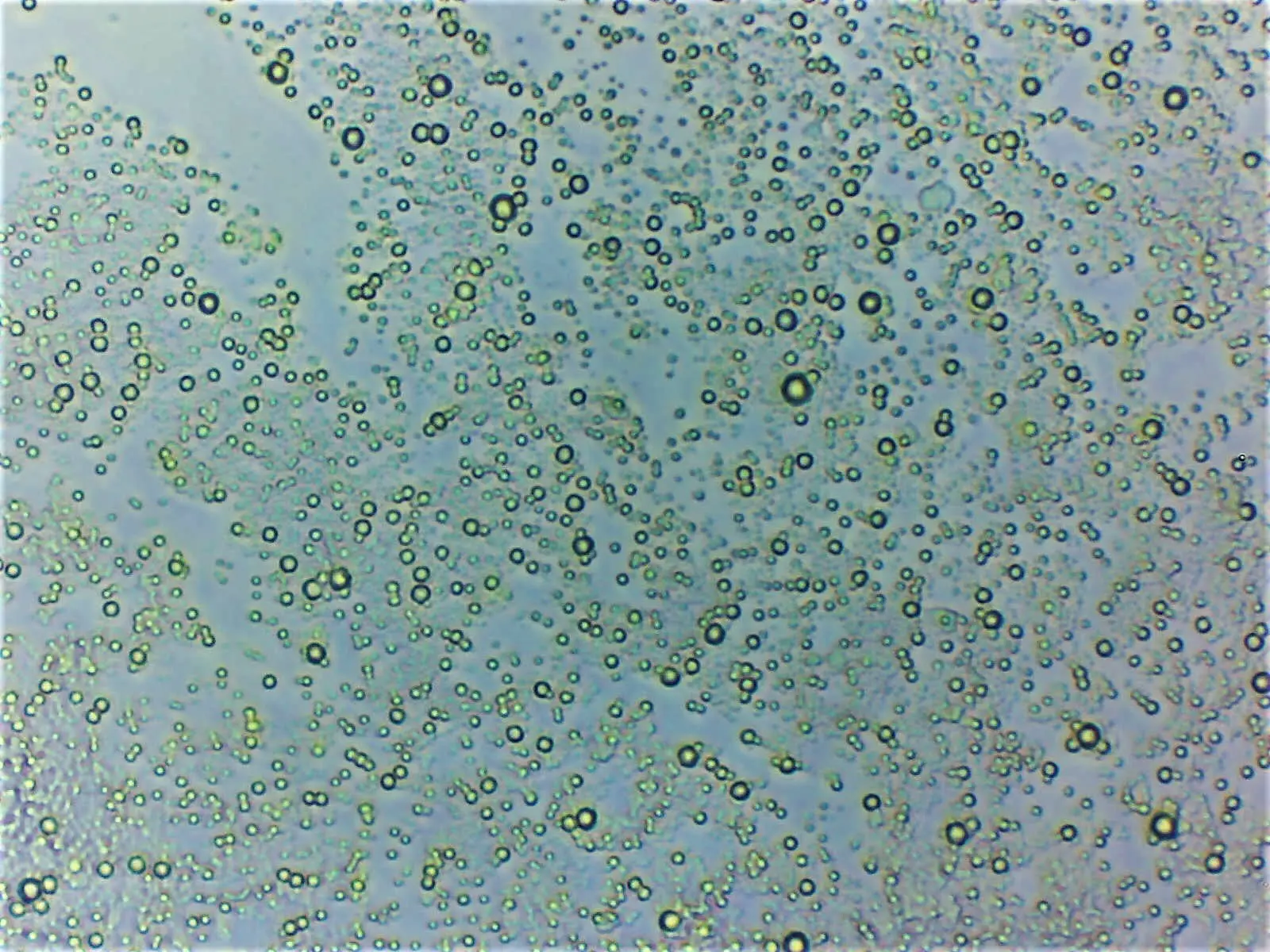Micrograph of cream showing its emulsion structure. As the oil droplets are less dense than the water surrounding them they tend to float (credit: edibotopic).