Drawing Structures from Notation
I created a program in the Racket programming language to draw diagrams based on a symbolic notation that describes the topology of physical systems.
Background
Dispersed Systems
A lot of science and engineering concerns dispersed systems. In this context, system relates to there being many parts comprising the whole. Dispersed refers to sets of parts that are distributed randomly in space, usually in large number.
Important materials are often dispersions, in which there is one set of parts dispersed in a continuous matrix. These include liquid foams (e.g., gas bubbles in water), emulsions (e.g., oil droplets in water) and gels (e.g., water droplets in solid).
These dispersion often have characteristic qualities that are useful to us. In food, emulsions can simultaneously carry water- and oil-soluble nutrients, and opacity is generated by the thousands of oil droplets scattering light. Dispersions like emulsions and suspensions are also intrinsically unstable, separating over time depending on properties like particle size and solvent viscosity.
DSF Formalism
Talking about dispersed systems can get difficult quickly. This is because many of them contain sub-systems with their own distinct topologies. At one level, bread crumb is a solid foam, with gas bubbles dispersed in a solid matrix. Zooming out, this foam is enclosed in a solid crust. Zooming back in, the solid matrix is itself a dispersion of starch granules. The following is a mouthful:
A dispersion of bubbles in a dispersion of starch granules enclosed in a solid container
For this reason, the Dispersed System Formalism (DSF) was invented by the French scientist Hervé This.
For decades scientists have referred to oil-in-water emulsions using the following notation:
$$O/W$$
The letters refer to physical phases — O(il) and W(ater) — and the forward slash refers to the relation dispersed in. In most cases, DSF simply extends this notation to encompass a broader class of phases and larger set of relations. Obviously, a liquid foam could be represented as:
$$G/W$$
If a foam is enclosed in a solid we need an additional character for S(olid) and an additional operator for enclosure (@):
$$(G/W)@S$$
The apparatus of DSF has further intricacies, elaborated in academic papers Prof This has written on the topic. For now, this is enough to get started.
DSF-racket
DSF-racket is a racket module (more correctly: two modules) that can be imported into racket projects. It allows diagrams to be drawn using DSF notation with dsf.rkt and tree representations of DSF structures to be drawn with tree.rkt.
Motivation
When DSF notation is used it is often necessary to include diagrams. People might not be familiar with the notation and visualisation helps. This is also common in similar fields like spatial logic, mereotopology and formal ontology. Philosophers, ontologists and computer scientists in these areas rely on symbolic tools like formal logic and set theory to represent space, but their papers are also filled with explanatory diagrams.
It seems to me that a tighter coupling between the symbolic and diagrammatic representations could be fruitful for three reasons:
It reduces the workload on the communicator, as diagrams do not have to be created separately from the notation.
It creates a learning tool, as manipulation of the symbols generates diagrams as feedback for the learner.
It ensures consistency, as two individuals writing the same notation should always generated an equivalent diagram.
How it Works
Symbolising Regions of Space
The Racket language, like most Lisp dialects, uses prefix notation. Instead of writing the expression 2 + 3 to get the value 5, we write:
(+ 2 3)
Individual expressions are wrapped in parentheses.
In DSF, O+W means effectively:
Take oil and take water
or
The mixture of oil and water
Topologically, it means that the two phases are disconnected from each other in the system. Here and a few other places I deviate from the DSF notation slightly, preferring the symbol $:$ to signify disconnection:
(: o w)
If (+ 2 3) returns 5 what does (: o w) do? It draws a diagram showing two circles with different colours that are disconnected.

To enclose the structure in a solid:
(@ (: o w) S)
If you are unfamiliar with prefix notation this might seem confusing, but it is not that difficult. Taking the inner-most parentheses, we have:
(mix oil with water)
The $@$ takes this mixture and encloses it in a container (signified by capital letter):
(enclose (mix oil with water) in Solid)
Again, this yields a diagram representing the structure:

Processes as Trees
One of the advantages of prefix notation is that it closely maps to a tree-like representation. The previous example of (@ (: o w) S) can be thought of as a process, consisting of nodes and connections between those nodes. Starting at the bottom of the tree, we would have nodes for oil (o) and water (w) which together connect to a mix node (:). This mix node then connects with the S(olid) container through an enclosure node (@).
A function is included in DSF-racket to draw such trees from notation. A structure can be stored as a list in a variable and then fed into the draw function:
'(@ (: o w) S)) ;; store in variable
(draw-tree myStructure) ;; call the draw function
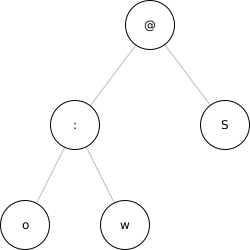
This can be especially useful when interpreting complex symbolic/diagrammatic representations, such as the following:
(: s (@ (@ (: o (& w g)) S) S))

Conceptual Aside: Dispersion
What is dispersion? It is a discrete set of particles in an enclosing container. What is dispersed is by definition a multiplicity: there has to be at least two regions of that material that are mutually disconnected from each other.
This means that to define and draw a dispersion we just need the $:$ and $@$ operators. For example, an emulsion of oil droplets in water is:
(@ (: o o) W)

Of course, many emulsions physically consist of thousands of oil droplets. We do not, however, need to represent thousands (or even three) droplets because the critical distinction is that between the continuous (one) and the discrete (two or more).
Operators in DSF-racket
Currently the following operators are defined (as functions):
| Symbol | Alias |
|---|---|
| : | mix |
| σ | connect |
| @ | enclose |
| & | overlap |
| ^ | m-connect |
Aliases are provided for more explicit formula definitions.
(equal? (mix oil gas) (: o g)) ;; #t
Binary
The operations briefly defined:
- Mix (
: x y) — x is disconnected from y - Connect (
σ x y) — x is externally connected to y - Enclose (
@ x Y) — x is enclosed in a container y - Overlap (
& x y) — x overlaps with y
Ternary
The idea of M(ediate)-connection was mentioned in Whitehead's Process & Reality.
- M-connect (
^ x y z): x is connected to y through z
Primitives
Atoms
| Symbol | Alias |
|---|---|
| g | gas |
| o | oil |
| s | solid |
| w | water |
Containers
| Symbol | Alias |
|---|---|
| G | Gas |
| O | Oil |
| S | Solid |
| W | Water |
Infix Notation
Racket supports a (somewhat verbose) form of infix notation. This involves the use of periods between an operation and its arguments:
(equal? (mix o g) (o . mix . g)) ;; #t
Why Racket?
Rapid Prototyping
I don't have much experience with Racket or Lisp. Despite this, I found it remarkably simple to get this project functioning in a single afternoon.
Racket installs with an IDE called DrRacket and several built-in libraries. Writing the following into the editor is sufficient to generate an image of a circle:
#lang racket ;;specify the language being used
2htdp/image) ;;use a built-in image library
(circle 20 "solid" "red") ;;circle with 20 px radius and solid red fill
I've played around a lot with programmatic graphics, and this is easily one of the quickest ways to get up and running. DrRacket has a REPL in the editor, making it convenient to quickly test any graphics that you define. There is an excellent tutorial for beginners that introduces basic programming concepts using Racket with pictures.
Early on, I opened a REPL and did something like this:
(circle 20 "solid" "red"))
(circle 20 "solid" "blue"))
(beside thing otherThing)
The beside function from 2htdp/image puts two shapes — as you might suspect — beside each other. In this case, the shapes connect (σ) at their boundary.
σ x y
(beside x y))
It got a little more complicated than this, but that was the basic idea.
Easy Distribution
Sharing a Racket program is not as convenient as sending a link to a web app, but it is compatible with different user environments.
It is trivial to use the DSF module if you have racket installed. After a git clone of the repository, the dsf folder can be copied to a racket project and then imported:
"dsf/base.rkt")
(@ w S) ;; will draw a diagram
If you are not using DrRacket then Emacs with Racket Mode installed/activated is a straight replacement.
Using the terminal or (Neo)Vim requires more work to preview images as you code.
Start a REPL in your terminal with:
To draw some diagrams you will need dsf/base.rkt and to render them to a frame you will need racket/gui/base and pict. Require them in the REPL:
"dsf/base.rkt")
racket/gui/base pict)
Now, entering the below code in the REPL will define a DSF formula and render the diagram in a separate frame:
(@ (@ (σ w o) S) W))
(show-pict myStructure)
Lastly, there is a Jupyter kernel for Racket — IRacket — that can be used to run Racket code in a Jupyter notebook.
If you have Jupyter and IRacket installed then DSF modules can be required as described previously and used to draw diagrams. Make sure that the kernel is set to Racket in your Jupyter instance.
Examples of how the module can be used in slide presentations (via Racket) and notebooks (via Jupyter) are included in the repo.
Next Steps
I have been fascinated with the general area of representing space (or more abstract regions) using symbolic languages for several years.
There are many people in disparate fields working on such problems, and I have been privately trying to connect ideas across these fields for some time.
DSF-racket is primarily focused on coupling symbolic and diagrammatic representations. I would like to extend the systems it can represent and to improve the quality of its diagrams, but it is largely feature-complete.
This post really only touches the surface on my thoughts on these formalisms, and I will likely revisit the area in the future.